2005 оноос хойш БҮТ нь улсын хэмжээнд нэгдсэн байдлаар ЭЕШ-ийг зохион явуулсан ба шалгуулагчдын амжилтыг анхны оноо, хэмжээст оноо, порценталь оноо гэсэн гурван үзүүлэлтээр эрэмбэлэн дүгнэж байна.
1. Анхны оноо гэж юу вэ? Энэ нь тухайн хичээлийн шалгалтын сэдэв даалгаврыг хэрхэн гүйцэтгэснийг илтгэх үнэлгээ бөгөөд авбал зохих онооноос хэдэн оноо авсныг хувьд шилжүүлсэн тоон үзүүлэлт юм. Тухайлбал, математик хичээлийн шалгалтын сэдэв нийт 50 оноотой ба шалгуулагч нийт 40 оноо цуглуулсан байг. Энэ нь анхны оноо болох бөгөөд хувьд шилжүүлэн тооцвол 80 хувийн гүйцэтгэлтэй шалгагджээ гэсэн үг юм. Анхны оноо нь хэмжээст оноог тооцон гаргах хамгийн чухал хамаарал юм.
2. Хэмжээст оноо ба проценталь оноо гэж юу вэ? Хэмжээст оноо гэдэг нь /ЭЕШ-ын батламж хуудас хоёр жил хүчинтэй тохиолдолд/ жил жилийн даалгаврын хүнд хөнгөний харьцааг тогтвортой байлгах зорилго бүхий олон улсын үнэлгээний аргачлал юм.
Дор дурдагдаж байгаа математикийн зарим ойлголтууд шалгуулагч та бүхэнд бүрхэг байвал мэргэжлийн багш нараасаа тусламж аваарай. Юуны өмнө хэвийн тархалтын талаар танилцуулъя. Хэвийн тархалт нь тусгай математик шинжүүдийг агуулсан тэгш хэмтэй тархалт юм. Энэ тархалт нь төрөл бүрийн статистик шийдвэр гаргахад өргөн хэрэглэдгээрээ ач холбогдолтой. Гэвч энэ тархалт бол онолын тархалт тул шалгуулагч та бүхний шалгалтын онооны тархалт нь яг хэвийн тархалттай байна гэсэн үг биш. Гэсэн хэдий ч шалгуулагчдын шалгалтад авсан онооны олон тархалт нь ойролцоогоор хэвийн тархалтад дөхөж очдог байна. Хэрэв шалгуулагчдын авсан онооны тархалт нь хэвийн тархалтаас өөр байвал уг тархалтыг урьдчилан математикийн тусгай аргын тусламжтайгаар тухайлбал шугаман биш хувиргалтыг хэрэглэж хэвийн тархалтруу шилжүүлдэг.
Зураг 1
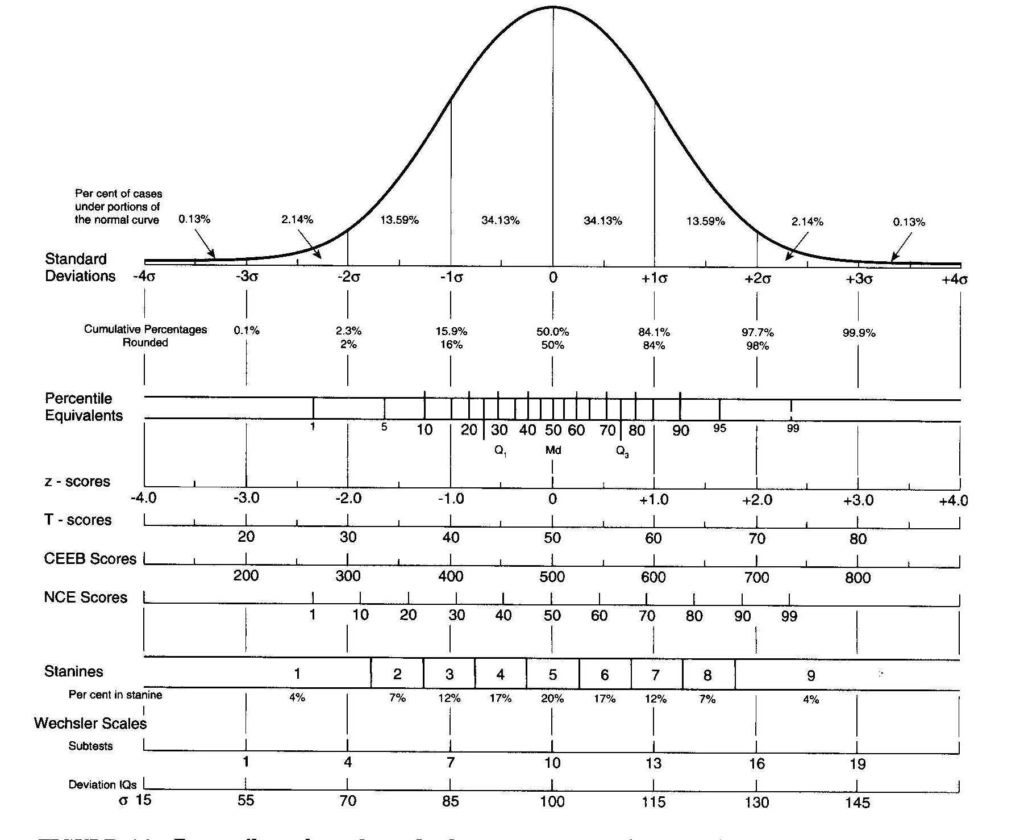
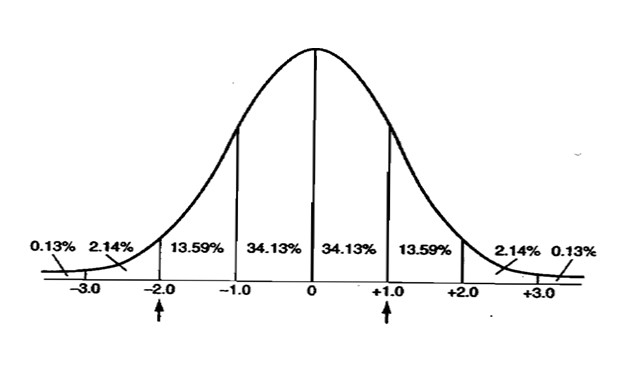
Зураг дээр хэвийн тархалтын муруй болон энэ тархалтын зарим шинжүүдийг үзүүллээ. Тухайлбал шалгуулагч та бүхний математикийн хичээлд үзсэн x ̅ – дундаж, моод – mode, медиан – MDN нэг цэгт давхцаж байна. Түүнчлэн зурагт үзүүлсэн хувиуд бол хэвийн тархалтын муруй доод хэсэгт ямар хэсгүүдэд онооны хэдэн хувь харьяалагдаж байгааг үзүүлсэн байна.
SD нь шалгуулагчдад шинэ ойлголт бөгөөд энэ нь дунджаасаа хазайх хазайлтыг илэрхийлдэг бөгөөд стандарт хазайлт гэж нэрлэдэг. Хэрэв зураг дээр үзүүлсэн хувиудыг нэмэх юм бол 99,9% нь [-3SD, +3SD] гэсэн интервалд харьяалагдаж байгааг та бүхэн ажиглах болно.
Зураг 2-г харвал энд бичигдсэн 34,13% нь дундаж ба түүнээс баруун талруу 1 стандарт хазайлт хоёрын хооронд орших онооны хувийг илэрхийлж байгаа юм. Жишээ нь: Хэрэв онооны тархалт маань 61 дундажтай, стандарт хазайлт нь 7 байх хэвийн тархалттай байсан гэж үзвэл энэ оноонуудын 34,13% нь [61, 61+7=68] гэсэн интервалын хооронд оршино гэсэн үг юм.
Зураг 2
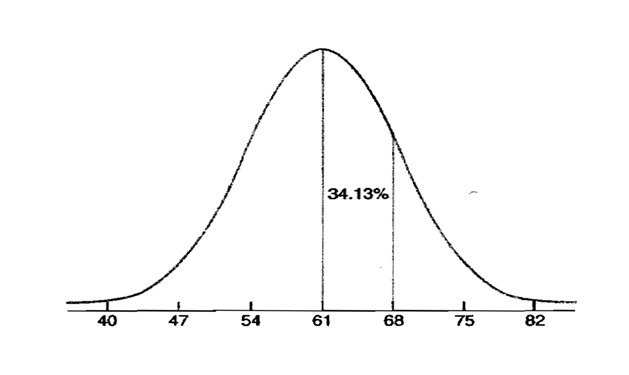
Хэрэв [54=61-7, 68=61+7] гэсэн интервалын хооронд онооны хэдэн хувь нь орших вэ? гэдгийг тооцоолбол 34%+34%=68% болохыг харж болно.
Зураг 3
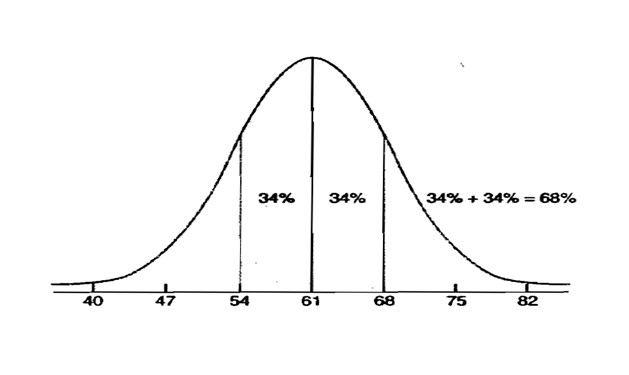
Хэвийн тархалтын муруйн тусламжтайгаар тодорхой өгөгдсөн онооны хувьд түүнээс дээш, эсвэл доош орших оноонуудын хувийг гаргаж болно. Тухайлбал 68 онооноос доош орших оноонуудын хувь нь ойролцоогоор 50%+34%=84% байна.
Зураг 4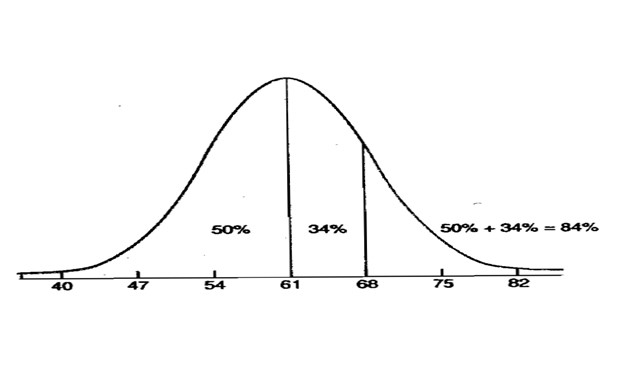
Энэ 84% процентыг 68 онооны проценталь гэж нэрлэдэг. Проценталь нь тухайн оноог авсан шалгуулагчийн нийт шалгуулагчдын дундах байр заадаг заадаг хэмжигдэхүүн юм. 2011 оноос эхлэн ЭЕШ-нд энэ проценталийг ашиглан шалгуулагчдын жагсаалтыг гаргаж байгаа учраас шалгуулагч та бүхэнд энэ талын ойлголтыг өгөх үүднээс дээрх анхдагч ойлголтыг өгч байна.
Сая бид зөвхөн шалгуулагчдын тестен дээр авсан анхдагч онооны тархалтын талаар ярилцлаа. Өөрөөр хэлбэл шалгуулагч бүрийн шалгалтуудад авсан оноо нь өөр өөр дундаж, стандарт хазайлт бүхий тархалтад харьяалагддаг болохыг мэдэж авлаа. Одоо бид өөр өөр хичээлүүд дээр авсан тестийн анхдагч оноонуудыг яаж харьцуулах вэ? гэдгийн авч үзье. Жишээ нь: Шалгуулагч Дулам математикийн шалгалтад 85, англи хэлний шалгалтад 90 оноо авсан гэж үзье. Тэгвэл Дулам аль хичээл дээр нь илүү амжилт үзүүлсэн бэ? Энэ асуултад хариулахын тулд бидэнд нэмэлт мэдээлэл хэрэгтэй болно. Тухайлбал математикийн болон англи хэлний хичээл дээр шалгуулагчдын авсан онооны тархалтыг мэдэх хэрэгтэй. Дээрх жишээний дагуу Дуламын өгсөн хоёр шалгалтын оноонуудын тархалтын дунджууд ба стандарт хазайлтууд нь өгөгдсөн гэж үзье.
Математик Англи хэл
Оноо x=85 x=90
Дундаж (x) ̅=75 (x) ̅=140
Стандарт хазайлт SD=10 SD=25
Хэрэв онооны тархалтуудыг хэвийн гэж үзвэл дараах зургийг гаргаж авна.
Зураг 5
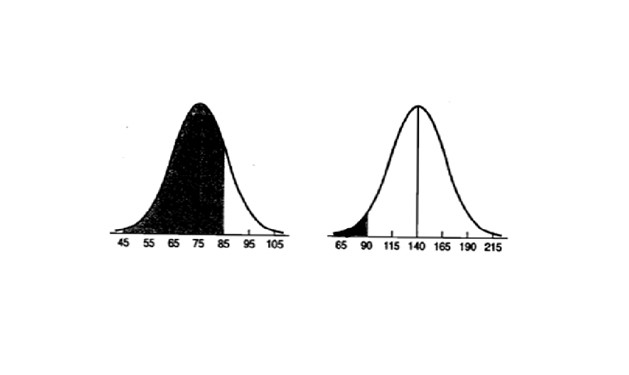 Математик Англи хэл
Математик Англи хэл
Зурагт үзүүлсэн хараар будагдсан хэсгийн талбай нь Дуламын авсан онооноос доош оноо авсан шалгуулагчдын хувийг үзүүлж байна. Өөрөөр хэлбэл проценталиуд юм. Тухайн шалгалтууд өгсөн шалгуулагчидтай харьцуулахад математикийн хичээл дээр 84% нь Дуламаас доогуур үзүүлэлттэй Англи хэлний хичээл дээр 2% нь доогуур үзүүлэлттэй байна. Үүнийг тодорхойлохын тулд Z- оноог ашигладаг.
![]() Энэ хувиргалтыг ашиглан Дуламын Z- оноог гаргая.
Энэ хувиргалтыг ашиглан Дуламын Z- оноог гаргая.
![]()
![]()
Зураг 6
Математик Англи хэл
Эндээс харах юм бол Дуламын аль хичээл дээр илүү амжилт үзүүлснийг тодорхойлж болно. Тухайлбал: Математикийн хичээл дээр +1.0, англи хэлний хичээл дээр -2.0 оноо авсан байна. Өөрөөр хэлбэл математикийн хичээл дээр +1.0 оноотойгоор илүү амжилт үзүүлжээ. Шалгуулагчдыг энэ Z – оноогоор жагсаахад багахан тохиромжгүй байдаг. Учир нь Z -оноо нь хасах, нэмэх тэмдэгтэй байхаас гадна аравтын бутархайгаар илэрхийлэгддэг. Иймд үүнээс гарахын тулд ЭЕШ-нд 500 дундажтай, стандарт хазайлт нь 100 байх хэвийн тархалтруу Z – оноог шилжүүлдэг. Энэ шилжүүлсэн оноог хэмжээст оноо гэх бөгөөд X=500+100xZ хувиргалт хийдэг. Энэ тохиолдолд [200, 800] интервалын хооронд шалгалт өгсөн шалгуулагчдын 99,97% нь харьяалагдахыг та бүхэн дээрх ойлголтуудаас мэдэж авсан байх гэж бодож байна. Одоо шалгуулагч Дулам нь математикийн хичээл дээр 500+100×1=600, англи хэлний хичээл дээр 500+100x(-2) = 300 хэмжээст оноонуудыг авчээ. Эцэст нь шалгуулагч Дуламын оноонуудыг бичвэл:
| Үнэлгээний хэмжигдэхүүн |
Математик |
Англи хэл |
|
| Анхны оноо |
85 |
90 |
|
| Хэмжээст оноо |
600 |
300 |
|
| Проценталь |
84% |
2% |
байна. Дашрамд сонирхуулахад шалгуулагч та бүхний сонирхдог IQ тестийн хувьд дундаж нь 100, стандарт хазайлт нь 15 байх X=100+15xZ гэсэн хувиргалтыг ашигладаг.













